HomeWikiPrandtl-Tomlinson friction model
January, 8 2025
Prandtl-Tomlinson friction model
Table of Contents
The Prandtl–Tomlinson model was introduced in 1928 as a conceptual framework for single-atom contact friction, described as a point mass dragged over a sinusoidal potential by a spring. Although it remained largely overlooked for decades, recent experimental validations have demonstrated its relevance for contacts involving tens to hundreds of atoms. Today, the Prandtl–Tomlinson model is widely recognized as a highly insightful mechanical analogue for understanding atomic-scale phenomena at sliding interfaces.
The field of nanotribology emerged in the late 1980s which was a significant leap in friction research by enabling the study of nanoscale contacts with tools like the atomic force microscope (AFM). Among its notable breakthroughs was the observation of individual atomic “hopping events” over a corrugated interface potential with atomic periodicity. These events revealed a “stick-slip” motion that revitalized interest in the Prandtl−Tomlinson (PT) model, an older conceptual framework. Historically, the PT model is often attributed to G. A. Tomlinson’s 1929 paper, which led to its alternate name, the “Tomlinson model.” However, the theory underlying the PT model was first presented in Ludwig Prandtl’s 1928 paper, which was initially inaccessible to much of the scientific community due to its publication in German. This oversight was corrected in 2012, when an English translation of Prandtl’s seminal work was published, finally clarifying its foundational role in modern nanotribology.
The PT model today forms the cornerstone of our understanding of atomic-scale friction. In this model, a point mass moves over a periodic potential (illustrated in Figure 1), explaining a wide range of experimental observations.
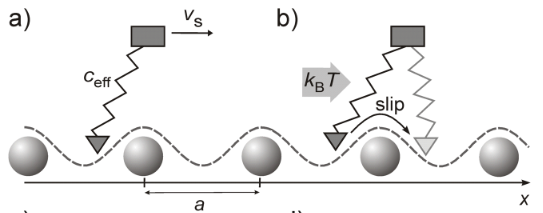
Figure-1 Schematic drawing illustrating the basic principles of the Prandtl−Tomlinson model.
This schematics in Figure-1 a) and b) shows the basics of PT model, where a point mass is connected to a supporting body M via a spring with an effective spring constant ceff. The mass interacts with a periodic potential V(xt) with a periodicity ‘a’. During sliding, the supporting body M moves with a velocity vS in the x-direction. If the spring is sufficiently soft, the resulting motion exhibits characteristic “stick-slip” behavior. The point mass remains in a potential minimum (“stick”) until the spring tension reaches a critical value, at which point it jumps (“slips”) to the next minimum. The model also predicts temperature effects, which can be introduced by considering thermal oscillations of the mass.
Figure-2 Graphs showing the scan position with lateral force wit changes in temperature
Figure-2 c and d show at zero temperature (T=0K), the lateral force is a sawtooth-like function, with the mass jumping only when the critical force Fc for that potential and spring constant is reached. The lateral force is measured by tracking the spring tension as a function of the position of the supporting body M along the x-axis (“scan position”), which differs from the tip’s position xt. At higher temperatures, thermal activation allows the mass to jump at forces lower than Fc, due to thermal energy kBT (where kB is Boltzmann’s constant). As a result, the maxima of the lateral force and the overall frictional force decrease, and thermal noise becomes visible on the “rising leg” of the sawtooth pattern.
Figure-3 ketch of a mechanical model designed by Prandtl
The schematics of Figure 3 shows a macroscopic mechanical model created by Prandtl to demonstrate stick-slip behavior same as that of the atomic-scale model, illustrating the generalizability of the concept. The PT model has successfully explained friction phenomena across various systems, including flat surfaces, surfaces with different atom types, velocity and temperature dependence, atomic-scale steps, and ions in a trap. Notably, despite its origins as a single-atom model, the PT model provides intuitive explanations for many fundamental properties of dry friction.
Extrapolation to Macroscopic Scale: While the PT model effectively explains friction at the atomic scale, it remains challenging to extrapolate its findings to larger, macroscopic contacts. Scaling up from nanometre-sized contacts to macroscopic rough interfaces has not yet been fully resolved. This limitation stems from the difficulty in translating atomic-scale behaviours into statistical models for complex, rough contact surfaces.
Complexity of Real-World Surfaces: The PT model primarily addresses idealized, single-atom contacts. In real-world applications, surfaces are often non-ideal, featuring defects, surface steps, impurities, and varying chemical activities. These factors influence friction and are not adequately captured by the simple model, limiting its applicability to more complex systems.
Structural Lubricity and Super-Lubricity: Although phenomena like “structural lubricity” or “super-lubricity” have been observed at atomic and small-scale contacts, the PT model does not fully account for how friction behaves in the presence of these phenomena when the contact area is large. The scaling of friction with contact area remains a significant challenge, and the model’s predictions for real, rough contacts are still incomplete.
References:

I am a postgraduate researcher at the University of Leeds. I have completed my master's degree in the Erasmus Tribos program at the University of Leeds, University of Ljubljana, and University of Coimbra and my bachelor's degree in Mechanical Engineering from VTU in NMIT, India. I am an editor and social networking manager at TriboNet. I have a YouTube channel called Tribo Geek where I upload videos on travel, research life, and topics for master's and PhD students.